/Szkoła średnia/Zadania maturalne/Matura 2009/Matura próbna/CKE
Próbny Egzamin Maturalny
z Matematyki poziom rozszerzony 13 stycznia 2009 Czas pracy: 180 minut
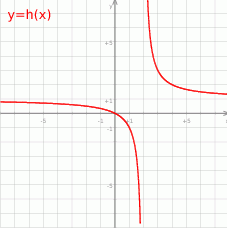
Na rysunku narysowano fragment wykresu funkcji 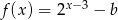 , określonej dla
, określonej dla 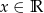 .
.
- Podaj wartość
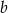 .
. - Naszkicuj wykres funkcji
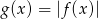 .
. - Podaj wszystkie wartości parametru
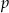 , dla których równanie
, dla których równanie 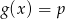 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
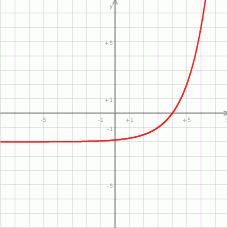
Rozwiąż nierówność 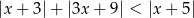 .
.
Jeden z końców odcinka leży na paraboli 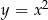 , a drugi na prostej o równaniu
, a drugi na prostej o równaniu 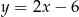 . Wykaż, że długość tego odcinka jest nie mniejsza od
. Wykaż, że długość tego odcinka jest nie mniejsza od 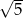 . Sporządź odpowiedni rysunek.
. Sporządź odpowiedni rysunek.
Oblicz prawdopodobieństwo 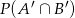 , jeśli
, jeśli 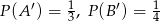 i
i 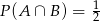 .
.
Na rysunku przedstawiono fragment wykresu funkcji 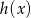 otrzymanego przez przesunięcie o wektor
otrzymanego przez przesunięcie o wektor ![[2,1]](https://img.zadania.info/zes/0077458/HzesT15x.gif) wykresu funkcji
wykresu funkcji 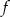 określonej wzorem
określonej wzorem 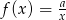 , dla
, dla 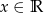 i
i 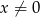 .
.
Wyznacz wzór funkcji  , a następnie sprawdź, czy punkt
, a następnie sprawdź, czy punkt 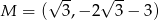 należy do jej wykresu.
należy do jej wykresu.
Porównaj liczby 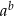 i
i 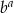 , gdzie
, gdzie ![[ √ --1 √ --1] 2 a = (2 − 3)2 + (2 + 3)2](https://img.zadania.info/zes/0077458/HzesT25x.gif) ,
, 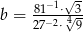 .
.
Dane jest równanie ![(x + 3)[x2 + (p + 4)x + (p + 1)2] = 0](https://img.zadania.info/zes/0077458/HzesT27x.gif) z niewiadomą
z niewiadomą  .
.
- Rozwiąż to równanie dla
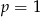 .
. - Wyznacz wszystkie wartości parametru
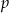 , dla których równanie to ma tylko jedno rozwiązanie.
, dla których równanie to ma tylko jedno rozwiązanie.
Trapez równoramienny jest opisany na okręgu. Suma długości krótszej podstawy i ramienia trapezu jest równa 30. Wyraź pole tego trapezu jako funkcję długości jego ramienia. Wyznacz dziedzinę tej funkcji.
Środek okręgu przechodzącego przez punkty 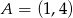 i
i 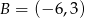 leży na osi
leży na osi 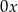 .
.
- Wyznacz równanie tego okręgu.
- Wyznacz równanie prostej prostopadłej do prostej
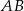 i oddalonej od początku układu współrzędnych o
i oddalonej od początku układu współrzędnych o 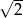 .
.
Sinusy kątów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ze sobą ciąg geometryczny. Oblicz sinus najmniejszego kąta tego trójkąta.
Dany jest ostrosłup prawidłowy czworokątny, w którym wszystkie krawędzie mają równą długość. Zaznacz na rysunku kąt utworzony przez dwie sąsiednie ściany boczne tego ostrosłupa i oblicz cosinus tego kąta.