/Szkoła średnia/Zadania maturalne/Matura 2009/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez portal www.zadania.info poziom rozszerzony 21 marca 2009 Czas pracy: 180 minut
Niech 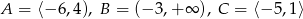 . Wyznacz zbiór
. Wyznacz zbiór 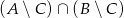 .
.
Dla każdej liczby rzeczywistej  obliczamy różnicę sześcianów liczb: o 1 mniejszej od
obliczamy różnicę sześcianów liczb: o 1 mniejszej od  oraz o 2 większej od
oraz o 2 większej od  . Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
. Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
Trzywyrazowy ciąg geometryczny jest rosnący. Iloczyn wszystkich wyrazów tego ciągu jest równy -8, a iloraz pierwszego wyrazu przez trzeci wynosi 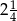 . Wyznacz ten ciąg.
. Wyznacz ten ciąg.
Długości  i
i 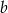 przyprostokątnych trójkąta prostokątnego spełniają równość
przyprostokątnych trójkąta prostokątnego spełniają równość
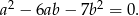
- Oblicz tangensy kątów ostrych tego trójkąta.
- Uzasadnij, że pole tego trójkąta jest równe
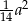 .
.
Z cyfr 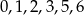 tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
Dany jest wielomian 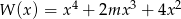 z parametrem
z parametrem 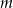 .
.
- Wiedząc, że wykres tego wielomianu jest symetryczny względem prostej
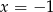 , wyznacz
, wyznacz 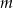 .
. - Dla wyznaczonej wartości parametru
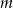 uzasadnij, że nierówność
uzasadnij, że nierówność 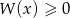 jest spełniona przez każdą liczbę rzeczywistą
jest spełniona przez każdą liczbę rzeczywistą 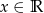 .
.
Punkty 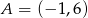 i
i 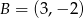 są wierzchołkami trójkąta
są wierzchołkami trójkąta 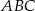 . Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne
. Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne 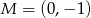 oblicz współrzędne wierzchołka
oblicz współrzędne wierzchołka 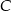 .
.
O liczbach  i
i 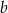 wiadomo, że
wiadomo, że 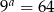 oraz
oraz 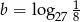 . Oblicz
. Oblicz 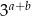 .
.
Dane jest równanie 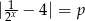 z parametrem
z parametrem 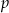 . Wyznacz liczbę rozwiązań tego równania w zależności od parametru
. Wyznacz liczbę rozwiązań tego równania w zależności od parametru 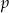 .
.
W czworościanie 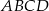 krawędź
krawędź 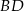 ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
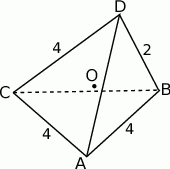
- Oblicz odległość krawędzi
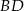 od krawędzi
od krawędzi 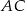 .
. - Wiedząc, że punkt
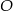 jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka
jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka 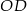 .
.
Ciąg 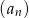 określony jest wzorem
określony jest wzorem 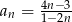 , dla
, dla 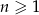 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 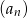 różni się od liczby -2 o więcej niż 0,1.
różni się od liczby -2 o więcej niż 0,1.

