Zadanie nr 6976133

Rozwiąż równanie 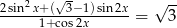2sin2x+ (√3−1)sin 2x √ -- -----1+-cos2x------= 3 .

Rozwiązanie

Oczywiście musi być 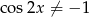cos2x ⁄= − 1 . Równie przekształcamy korzystając ze wzorów

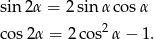
sin 2α = 2sinα cos α cos2α = 2co s2α − 1.

Mamy więc

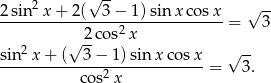
√ -- 2sin2x + 2 ( 3− 1)sinx cos x √ -- ----------------2--------------= 3 √ 2-cos x sin-2x-+-(--3-−-1)sin-xco-sx- √ -- cos2x = 3.

Dalsze przekształcenia wykonamy na dwa sposoby.

Sposób I

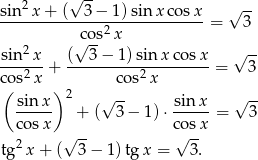
-- sin2 x + (√ 3− 1)sin xco sx √ -- --------------2-------------= 3 c√o-s x sin-2x- (--3−--1)sinx-cos-x- √ -- cos2x + co s2x = 3 ( )2 -- -- sin-x- + (√ 3 − 1) ⋅ sin-x = √ 3 cosx cos x 2 √ -- √ -- tg x + ( 3 − 1) tg x = 3 .

Możemy teraz podstawić 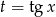t = tg x .

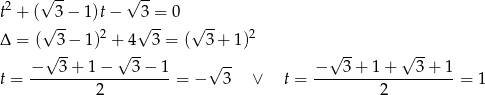
√ -- √ -- t2 + ( 3 − 1)t − 3 = 0 √ -- √ -- √ -- Δ = ( 3− 1 )2 + 4 3 = ( 3+ 1)2 √ -- √ -- √ -- √ -- √ -- t = −---3+--1−----3−--1 = − 3 ∨ t = −---3+--1+----3+--1 = 1 2 2

Zatem

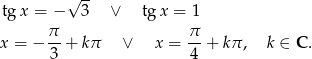
√ -- tgx = − 3 ∨ tgx = 1 π π x = − -- + kπ ∨ x = -- + kπ , k ∈ C . 3 4

Na koniec powinniśmy sprawdzić, czy otrzymane rozwiązania należą do dziedziny równania, tzn. czy 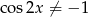co s2x ⁄= − 1 – łatwo sprawdzić, że tak jest.

Sposób II

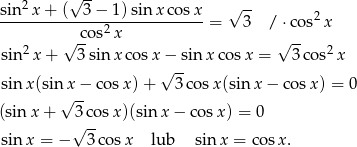
2 √ -- √ -- sin--x-+-(--3-−-1)-sin-xc-osx-= 3 / ⋅co s2x √ -cos2x √ -- sin 2x + 3 sin x cosx − sin xco sx = 3 cos2 x √ -- sin x(sin x− cosx )+ 3cos x(sinx − co sx) = 0 √ -- (sin x+ 3√co-sx)(sin x− cosx ) = 0 sin x = − 3cos x lub sin x = cos x.

Dzielimy każde z równań przez 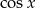cosx i mamy

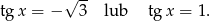
√ -- tg x = − 3 lub tgx = 1.

Otrzymane równania rozwiązujemy tak samo jak w pierwszym sposobie.
Odpowiedź: x = − π3-+ kπ ∨ x = π4-+ kπ , k ∈ C