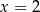Zadanie nr 1183609
Wyznacz największą liczbę całkowitą spełniającą nierówność: 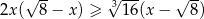 .
.
Rozwiązanie
Przekształcamy daną nierówność
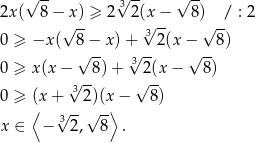
Ponieważ 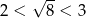 , największą liczbą całkowitą spełniającą tą nierówność jest
, największą liczbą całkowitą spełniającą tą nierówność jest 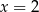 .
.
Odpowiedź: 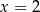
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz największą liczbę całkowitą spełniającą nierówność: 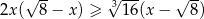 .
.
Przekształcamy daną nierówność
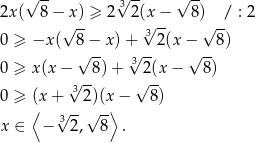
Ponieważ 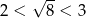 , największą liczbą całkowitą spełniającą tą nierówność jest
, największą liczbą całkowitą spełniającą tą nierówność jest 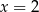 .
.
Odpowiedź: