Zadanie nr 2426255
Wyznacz te wartości parametru  , dla których zbiorem rozwiązań nierówności
, dla których zbiorem rozwiązań nierówności 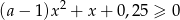 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych.
Rozwiązanie
Jeżeli równanie jest linowe, czyli 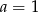 , to mamy nierówność
, to mamy nierówność 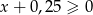 , która oczywiście nie jest spełniona przez wszystkie liczby rzeczywiste.
, która oczywiście nie jest spełniona przez wszystkie liczby rzeczywiste.
Dla 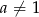 , mamy nierówność kwadratową. Jeżeli mają ją spełniać wszystkie liczby rzeczywiste, to ramiona paraboli będącej jej wykresem muszą być skierowane do góry, czyli
, mamy nierówność kwadratową. Jeżeli mają ją spełniać wszystkie liczby rzeczywiste, to ramiona paraboli będącej jej wykresem muszą być skierowane do góry, czyli 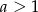 i
i 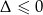 . Liczymy
. Liczymy
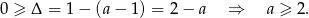
Mamay zatem 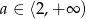 .
.
Odpowiedź: