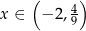/Szkoła średnia/Nierówności/Kwadratowe

Zadanie nr 2648921

Dodaj do ulubionych
Dodaj do rozwiązanych

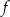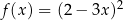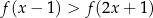Funkcja kwadratowa f jest określona wzorem 2 f (x) = (2 − 3x) . Wyznacz wszystkie argumenty x , dla których: f(x − 1) > f (2x+ 1) .

Rozwiązanie

Zauważmy najpierw, że

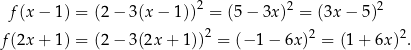
2 2 2 f(x − 1) = (2− 3 (x− 1)) = (5− 3x) = (3x − 5 ) 2 2 2 f(2x + 1) = (2− 3 (2x+ 1)) = (− 1− 6x) = (1 + 6x ) .

Pozostało więc rozwiązać nierówność

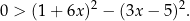
0 > (1 + 6x )2 − (3x − 5 )2.

Sposób I

Korzystamy ze wzoru skróconego mnożenia na różnicę kwadratów.

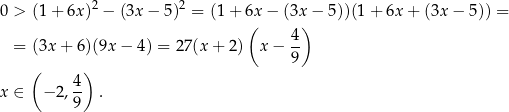
0 > (1 + 6x )2 − (3x − 5 )2 = (1+ 6x − (3x − 5))(1 + 6x + (3x − 5 )) = ( 4) = (3x + 6 )(9x− 4) = 27(x + 2 ) x− -- ( ) 9 4 x ∈ − 2,9- .

Sposób II

Rozwiązujemy nierówność

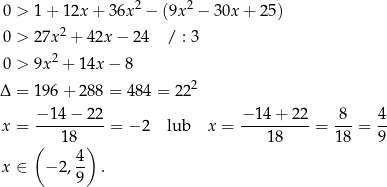
2 2 0 > 1 + 12x + 36x − (9x − 30x + 25) 0 > 27x 2 + 42x − 24 / : 3 2 0 > 9x + 14x − 8 2 Δ = 196 + 28 8 = 484 = 2 2 −-14-−-22- −1-4+-2-2- -8- 4- x = 18 = − 2 lub x = 18 = 1 8 = 9 ( 4) x ∈ − 2 ,-- . 9

 
Odpowiedź: ( ) x ∈ − 2, 49

Wersja PDF