/Szkoła średnia/Nierówności/Kwadratowe

Zadanie nr 3214710

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź wszystkie wartości 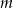m , dla których funkcja 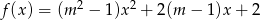2 2 f(x) = (m − 1)x + 2(m − 1)x + 2 przyjmuje wartość dodatnią dla każdej liczby rzeczywistej x .

Rozwiązanie

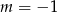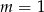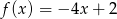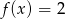Sprawdzamy najpierw co się dzieje gdy funkcja jest liniowa, czyli dla m = −1 lub m = 1 . Mamy wtedy f(x) = − 4x + 2 i f(x) = 2 . Druga z tych funkcji oczywiście spełnia podany warunek.

Jeżeli wykres funkcji 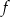f jest parabolą, to musi ona mieć ramiona skierowane do góry, czyli

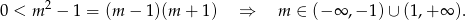
2 0 < m − 1 = (m − 1)(m + 1) ⇒ m ∈ (− ∞ ,− 1)∪ (1,+ ∞ ).

Ponadto nie może ona przecinać osi 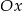Ox , czyli Δ < 0 .

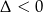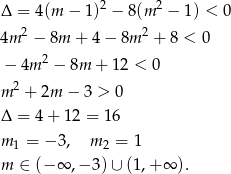
Δ = 4(m − 1)2 − 8(m 2 − 1) < 0 2 2 4m − 8m + 4− 8m + 8 < 0 − 4m 2 − 8m + 1 2 < 0 2 m + 2m − 3 > 0 Δ = 4 + 12 = 1 6 m 1 = − 3, m 2 = 1 m ∈ (− ∞ ,− 3)∪ (1,+ ∞ ).

Pozostało uwzględnić nierówność 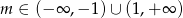m ∈ (− ∞ ,− 1)∪ (1 ,+ ∞ ) oraz fakt, że 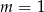m = 1 też jest dobrym rozwiązaniem. Mamy więc

m ∈ (− ∞ ,− 3)∪ ⟨1,+ ∞ ).

 
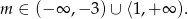
Odpowiedź: m ∈ (− ∞ ,− 3)∪ ⟨1,+ ∞ )

Wersja PDF