Zadanie nr 3639895
Dla jakich wartości parametru 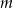 funkcja
funkcja
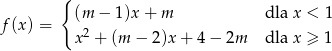
przyjmuje tylko dodatnie wartości?
Rozwiązanie
Zajmijmy się na początku pierwszą częścią wzoru. Ponieważ jest to funkcja liniowa to musi ona mieć współczynnik kierunkowy niedodatni (inaczej przyjmowałaby ujemne wartości) oraz musi mieć nieujemną wartość dla 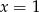 . Pierwszy warunek oznacza, że
. Pierwszy warunek oznacza, że 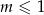 a drugi, że
a drugi, że
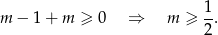
Oba warunki dają więc nam
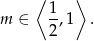
Zajmijmy się teraz drugą częścią wzoru. Jest to kawałek paraboli o ramionach skierowanych w górę. Aby jakoś zapisać kiedy ten kawałek jest powyżej osi 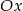 fajnie byłoby wiedzieć, gdzie jest jej wierzchołek – to jednak wiemy na mocy otrzymanej już nierówności
fajnie byłoby wiedzieć, gdzie jest jej wierzchołek – to jednak wiemy na mocy otrzymanej już nierówności
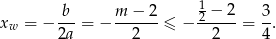
Zatem na przedziale 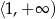 parabola ta jest rosnąca i aby była ona ponad osią wystarczy aby wartość w 1 była dodatnia. Liczymy
parabola ta jest rosnąca i aby była ona ponad osią wystarczy aby wartość w 1 była dodatnia. Liczymy
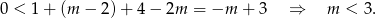
Odpowiedź: