/Szkoła średnia/Nierówności/Kwadratowe

Zadanie nr 3852475

Wyznacz największą liczbę całkowitą spełniającą nierówność

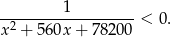
1 --2----------------< 0. x + 5 60x + 78200
Wersja PDF

Rozwiązanie

Oczywiście ułamek z lewej strony nierówności będzie ujemny dokładnie wtedy, gdy ujemny jest mianownik. Musimy więc rozwiązać nierówność

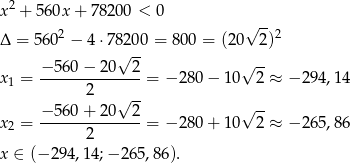
2 x + 560x + 7 8200 < 0 -- Δ = 5602 − 4 ⋅78200 = 800 = (20√ 2 )2 √ -- −5-60−--20--2- √ -- x1 = 2 = −2 80− 10 2 ≈ − 29 4,14 √ -- -- x = −5-60+--20--2-= −2 80+ 10√ 2 ≈ − 26 5,86 2 2 x ∈ (− 294,1 4;− 265,86).

Widać stąd, że największa liczba całkowita spełniająca tę nierówność to -266.  
Odpowiedź: -266

Wersja PDF