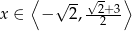Zadanie nr 6868468
Rozwiąż nierówność 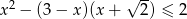 .
.
Rozwiązanie
Sposób I
Przekształcamy daną nierówność – korzystamy ze wzoru na różnicę kwadratów.
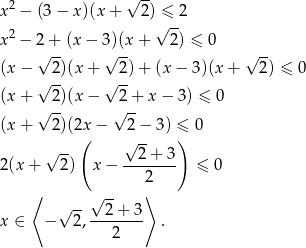
Sposób II
Przekształcamy daną nierówność
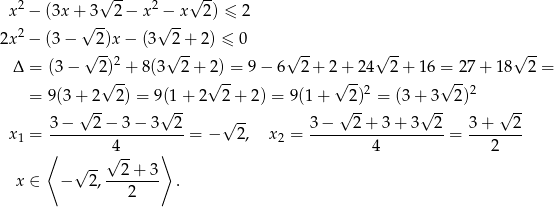
Odpowiedź: 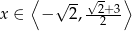
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 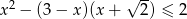 .
.
Sposób I
Przekształcamy daną nierówność – korzystamy ze wzoru na różnicę kwadratów.
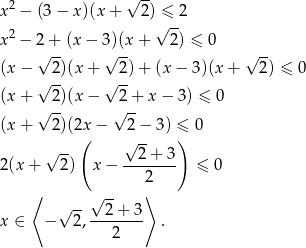
Sposób II
Przekształcamy daną nierówność
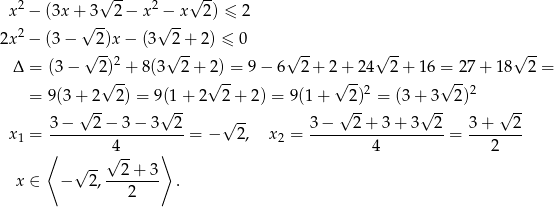
Odpowiedź: