/Szkoła średnia/Nierówności/Kwadratowe

Zadanie nr 9866123

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 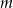m , dla których nierówność 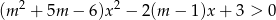(m 2 + 5m − 6)x2 − 2(m − 1 )x+ 3 > 0 jest prawdziwa dla każdego x ∈ R .

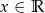Rozwiązanie

Sprawdźmy co się dzieje gdy nierówność jest liniowa, czyli gdy

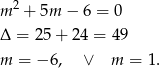
2 m + 5m − 6 = 0 Δ = 25+ 24 = 49 m = − 6, ∨ m = 1.

Dla 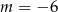m = − 6 mamy nierówność 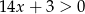14x + 3 > 0 , która nie spełnia podanego warunku. Dla 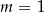m = 1 mamy nierówność 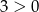3 > 0 , która jest zawsze spełniona.

Zajmijmy się teraz sytuacją, gdy wykresem lewej strony nierówności jest parabola. Aby była ona zawsze powyżej osi 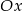Ox , musi mieć ramiona skierowane do góry oraz nie może mieć pierwiastków (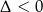Δ < 0 ). Pierwszy warunek daje nierówność

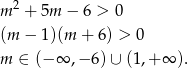
2 m + 5m − 6 > 0 (m − 1)(m + 6 ) > 0 m ∈ (− ∞ ,− 6)∪ (1,+ ∞ ).

Drugi warunek daje

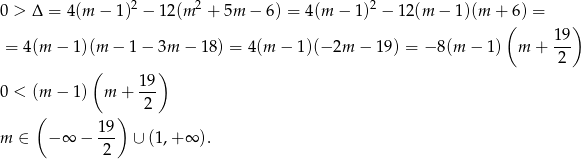
2 2 2 0 > Δ = 4(m − 1) − 12(m + 5m − 6) = 4 (m − 1) − 12(m − 1)(m + (6) = ) 1-9 = 4(m − 1)(m − 1 − 3m − 18) = 4(m − 1 )(−2m − 19) = − 8(m − 1) m + 2 ( ) 0 < (m − 1) m + 19- 2 ( 19 ) m ∈ − ∞ − --- ∪ (1,+ ∞ ). 2

Łącząc wszystkie otrzymane warunki mamy

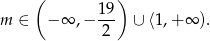
( ) 19- m ∈ − ∞ ,− 2 ∪ ⟨1,+ ∞ ).

 
Odpowiedź: ( 19) m ∈ − ∞ ,− 2 ∪ ⟨1,+ ∞ )

Wersja PDF