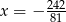/Szkoła średnia/Równania/Wielomianowe/Stopnia 5/Rozwiąż równanie

Zadanie nr 3843624

Rozwiąż równanie

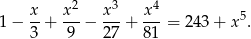
2 3 4 1− x-+ x--− x--+ x-- = 243 + x 5. 3 9 27 8 1
Wersja PDF

Rozwiązanie

Lewa strona jest sumą 5 początkowych wyrazów ciągu geometrycznego o ilorazie 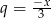q = −x3- . Ze wzoru na sumę początkowych wyrazów ciągu geometrycznego mamy więc równanie

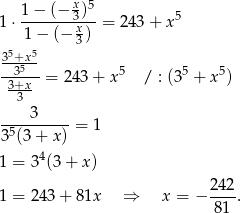
1-−-(−-x3)5 5 1 ⋅ 1− (− x) = 243 + x 5 5 3 3-+5x- -33+x--= 24 3+ x5 / : (35 + x5) 3 3 35(3+--x)-= 1 1 = 34(3+ x) 24 2 1 = 243 + 81x ⇒ x = − ----. 81

Do powyższego rachunku należy się kilka uwag. Po pierwsze wzór na sumę ma sens o ile 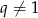q ⁄= 1 (bo jest 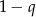1− q w mianowniku). Jednak dla 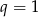q = 1 , czyli 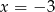x = − 3 mamy sprzeczną równość

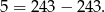
5 = 243 − 24 3.

Druga sprawa to dzielenie przez 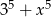35 + x5 . Ta liczba jest zero dokładnie dla 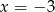x = − 3 , a ten przypadek przed chwilą rozważyliśmy.  
Odpowiedź: x = − 242- 81

Wersja PDF