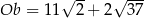/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Trapez

Zadanie nr 2353615

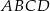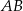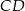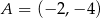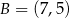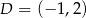Czworokąt ABCD jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki AB i CD , przy czym A = (− 2 ,− 4 ) , B = (7 ,5) i D = (− 1,2) , oblicz pole oraz obwód trapezu.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

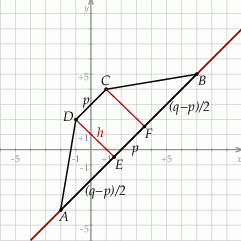
Widać, że od ręki możemy obliczyć długości: podstawy 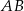AB i ramienia AD .

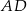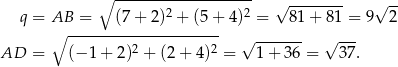
∘ ------------------- √ -------- √ -- q = AB = (7 + 2)2 + (5 + 4)2 = 8 1+ 8 1 = 9 2 ∘ --------------------- 2 2 √ ------- √ --- AD = (− 1+ 2) + (2+ 4) = 1+ 36 = 37 .

Powinno też być jasne jak obliczyć wysokość 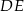DE trapezu – napiszemy równanie prostej 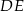DE , która jest prostopadła do 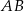AB i przechodzi przez 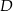D . To pozwoli wyznaczyć współrzędne punktu E .

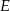Zacznijmy od prostej 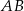AB – szukamy prostej w postaci 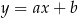y = ax + b i podstawiamy współrzędne punktów 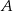A i B .

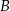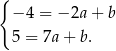
{ −4 = − 2a+ b 5 = 7a + b.

Odejmujemy od drugiego równania pierwsze i mamy 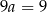9a = 9 , czyli 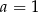a = 1 . Stąd 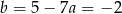b = 5− 7a = − 2 i prosta 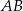AB ma równanie 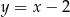y = x − 2 . To z kolei oznacza, że prosta 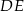DE (jako prostopadła do 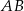AB ) ma równanie postaci 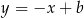y = −x + b . Współczynnik 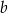b wyznaczamy podstawiając współrzędne punktu D .

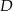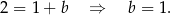
2 = 1+ b ⇒ b = 1.

Prosta 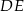DE ma więc równanie 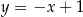y = −x + 1 . Szukamy teraz jej punktu wspólnego 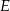E z prostą AB .

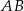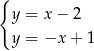
{ y = x − 2 y = −x + 1

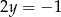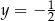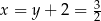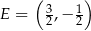Dodajemy równania stronami i mamy 2y = −1 , czyli 1 y = − 2 . Stąd x = y+ 2 = 3 2 i ( ) E = 3,− 1 2 2 . Wysokość trapezu jest więc równa

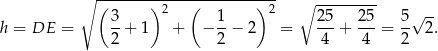
∘ ------------------------- ( ) 2 ( ) 2 ∘ --------- √ -- h = DE = 3-+ 1 + − 1-− 2 = 25+ 25-= 5- 2 . 2 2 4 4 2

Ponadto

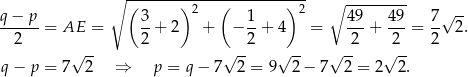
∘ (-------)2---(--------)-2 ∘ --------- q−--p- 3- 1- 49- 49- 7-√ -- 2 = AE = 2 + 2 + − 2 + 4 = 2 + 2 = 2 2. √ -- √ -- √ -- √ -- √ -- q − p = 7 2 ⇒ p = q − 7 2 = 9 2 − 7 2 = 2 2.

Pozostało obliczyć pole i obwód trapezu.

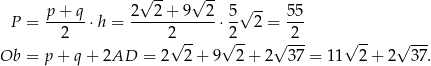
p+ q 2√ 2-+ 9 √ 2- 5√ -- 55 P = -----⋅ h = ------------⋅ -- 2 = --- 2 2√ -- √2-- √ 2-- √ -- √ --- Ob = p + q + 2AD = 2 2+ 9 2+ 2 37 = 11 2+ 2 37.

 
Odpowiedź: 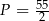55 P = 2 , √ -- √ --- Ob = 11 2+ 2 37

Wersja PDF