Zadanie nr 4392512
Odcinek o końcach 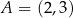 i
i 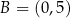 jest podstawą trapezu
jest podstawą trapezu 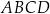 . Druga podstawa o środku w punkcie
. Druga podstawa o środku w punkcie 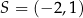 jest dwa razy dłuższa od podstawy
jest dwa razy dłuższa od podstawy 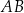 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 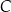 i
i 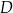 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
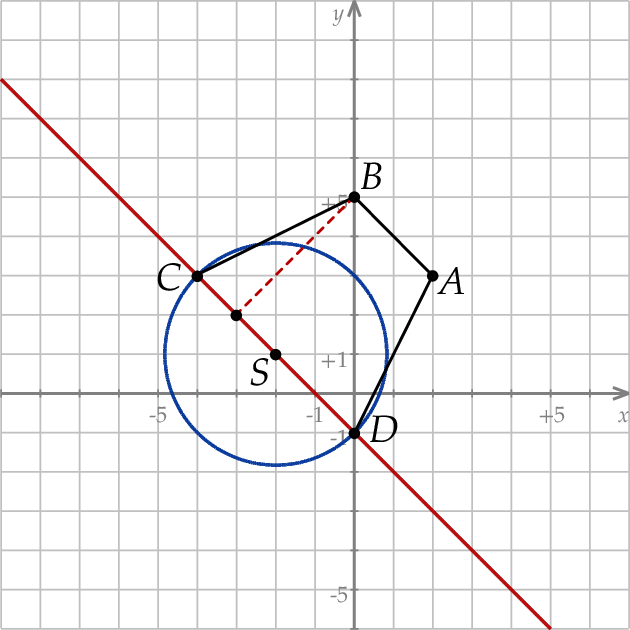
Zauważmy najpierw, że wiemy jaka jest długość podstawy 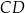
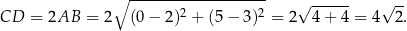
W takim razie punkty 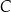 i
i 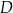 leżą na okręgu o środku
leżą na okręgu o środku 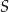 i promieniu
i promieniu 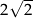 , czyli na okręgu
, czyli na okręgu
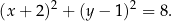
Oczywiście leżą one też na prostej równoległej do 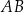 i przechodzącej przez
i przechodzącej przez 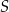 . Aby napisać równanie tej prostej, piszemy najpierw równanie prostej
. Aby napisać równanie tej prostej, piszemy najpierw równanie prostej 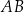 . Szukamy prostej w postaci
. Szukamy prostej w postaci 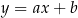 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 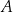 i
i 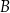 .
.
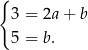
Z pierwszego równania mamy 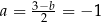 . W takim razie prosta
. W takim razie prosta 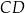 ma równanie postaci
ma równanie postaci 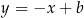 . Współczynnik
. Współczynnik 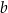 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 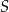 .
.
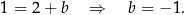
Zatem prosta 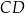 ma równanie
ma równanie 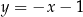 . Szukamy teraz punktów wspólnych tej prostej z wcześniej wyznaczonym okręgiem (podstawiamy
. Szukamy teraz punktów wspólnych tej prostej z wcześniej wyznaczonym okręgiem (podstawiamy 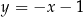 do równania okręgu).
do równania okręgu).
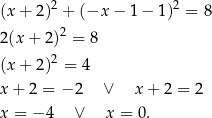
Mamy wtedy odpowiednio 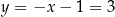 i
i 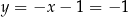 . Zatem
. Zatem 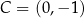 i
i 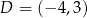 .
.
Aby obliczyć wysokość trapezu wystarczy obliczyć odległość punktu 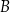 od prostej
od prostej 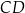 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 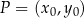 od prostej
od prostej 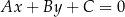 :
:
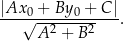
W naszej sytuacji mamy
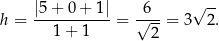
Pole trapezu jest więc równe
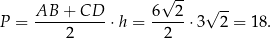
Odpowiedź: 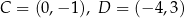 , pole:
, pole: 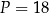 .
.

