Zadanie nr 4417558
Punkty 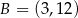 ,
, 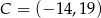 i
i 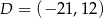 są kolejnymi wierzchołkami trapezu równoramiennego
są kolejnymi wierzchołkami trapezu równoramiennego 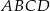 , który nie jest równoległobokiem, i w którym
, który nie jest równoległobokiem, i w którym 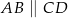 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 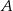 tego trapezu.
tego trapezu.
Rozwiązanie
Szkicujemy trapez.
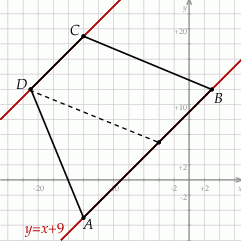
Plan jest taki: napiszemy równanie prostej 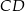 , potem równanie prostej
, potem równanie prostej 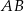 i na prostej
i na prostej 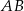 znajdziemy punkt
znajdziemy punkt 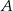 taki, że
taki, że 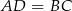 .
.
Do dzieła. Szukamy równania prostej 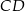 w postaci
w postaci 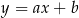 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 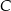 i
i 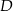 .
.
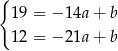
Odejmujemy od pierwszego równania drugie i mamy
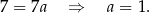
Współczynnik 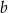 nie jest nam potrzebny. Teraz wyznaczamy prostą
nie jest nam potrzebny. Teraz wyznaczamy prostą 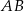 – jest ona równoległa do
– jest ona równoległa do 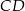 , więc ma równanie postaci
, więc ma równanie postaci 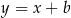 . Współczynnik
. Współczynnik 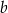 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 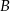 .
.

W takim razie prosta 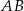 ma równanie postaci
ma równanie postaci 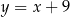 i współrzędne punktu
i współrzędne punktu 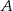 mają postać
mają postać 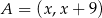 . Wiemy ponadto, że trapez jest równoramienny, więc
. Wiemy ponadto, że trapez jest równoramienny, więc
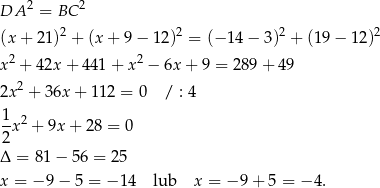
Zatem 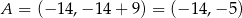 lub
lub 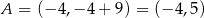 . To jeszcze nie całkiem koniec, bo z założenia trapez ma nie być równoległobokiem, czyli jego podstawy nie mogą mieć równych długości. Tymczasem, jeżeli
. To jeszcze nie całkiem koniec, bo z założenia trapez ma nie być równoległobokiem, czyli jego podstawy nie mogą mieć równych długości. Tymczasem, jeżeli 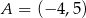 , to
, to
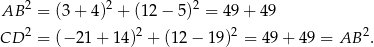
Zatem musi być 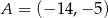 . Łatwo sprawdzić, że w tym przypadku
. Łatwo sprawdzić, że w tym przypadku 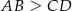 .
.
Odpowiedź: