Zadanie nr 6628114
Punkty 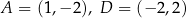 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 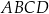 . Prosta
. Prosta 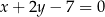 jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.
jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.
Rozwiązanie
Zaczynamy od rysunku.
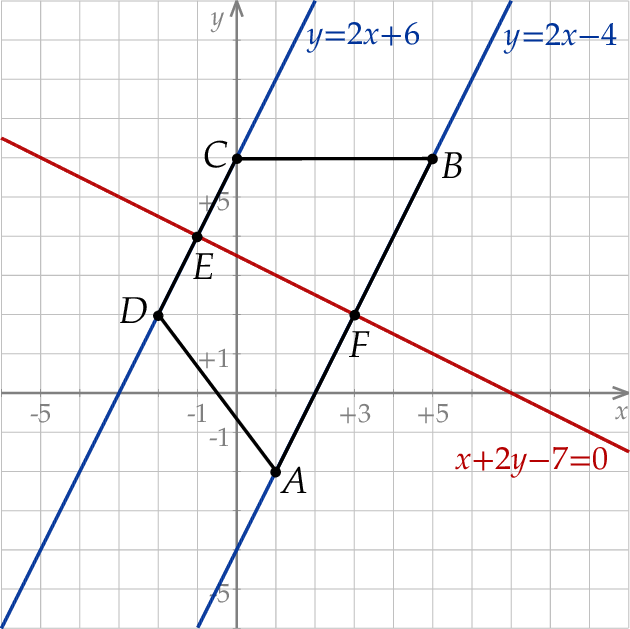
Na początku trochę trudno wyobrazić sobie jak ma wyglądać szukany trapez, ale ponieważ dana prosta nie przecina odcinka 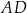 musi on być ramieniem trapezu, a prosta musi być osią symetrii prostopadłą do równoległych boków trapezu. W takim razie musimy znaleźć obraz odcinka
musi on być ramieniem trapezu, a prosta musi być osią symetrii prostopadłą do równoległych boków trapezu. W takim razie musimy znaleźć obraz odcinka 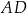 w symetrii względem danej prostej. Zrobimy to pisząc równania prostych, które są do niej prostopadłe i przechodzą przez punkty
w symetrii względem danej prostej. Zrobimy to pisząc równania prostych, które są do niej prostopadłe i przechodzą przez punkty 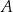 i
i 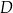 . Następnie znajdziemy na tych prostych punkty, które są odległe od danej prostej o tyle samo co punkty
. Następnie znajdziemy na tych prostych punkty, które są odległe od danej prostej o tyle samo co punkty 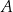 i
i 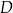 odpowiednio.
odpowiednio.
Dana prosta ma współczynnik kierunkowy 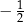 , więc proste do niej prostopadłe mają współczynnik kierunkowy 2. Znajdziemy teraz proste postaci
, więc proste do niej prostopadłe mają współczynnik kierunkowy 2. Znajdziemy teraz proste postaci 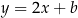 , które przechodzą odpowiednio przez punkty
, które przechodzą odpowiednio przez punkty 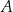 i
i 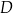 . Współczynnik
. Współczynnik 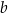 wyznaczamy podstawiając współrzędne tych punktów.
wyznaczamy podstawiając współrzędne tych punktów.
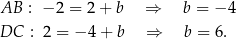
Zatem proste te mają odpowiednio równania 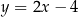 i
i 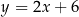 . Szukamy teraz punktów wspólnych tych prostych z daną prostą (od razy podstawiamy za
. Szukamy teraz punktów wspólnych tych prostych z daną prostą (od razy podstawiamy za 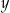 w jej równaniu).
w jej równaniu).
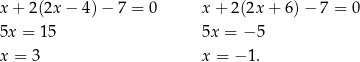
Daje to 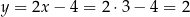 oraz
oraz 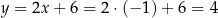 odpowiednio. Zatem
odpowiednio. Zatem 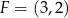 i
i 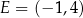 . Teraz wystarczy zauważyć, że punkty
. Teraz wystarczy zauważyć, że punkty 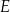 i
i 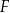 są środkami odcinków
są środkami odcinków 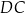 i
i 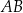 odpowiednio. Zatem
odpowiednio. Zatem
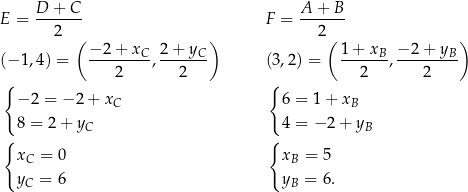
Zatem 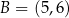 i
i 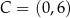 .
.
Odpowiedź: