Zadanie nr 7996999
Punkty 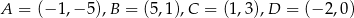 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 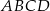 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Rozwiązanie
Rozpoczynamy oczywiście od szkicowego rysunku.
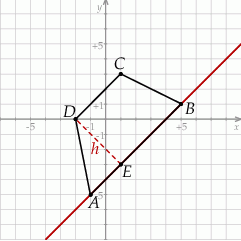
Aby obliczyć pole trapezu musimy znać długości jego podstaw oraz długość wysokości. Długości podstaw łatwo obliczyć.
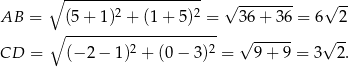
Napiszmy teraz równanie prostej 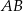 . Szukamy prostej w postaci
. Szukamy prostej w postaci 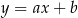 . Podstawiamy współrzędne punktów
. Podstawiamy współrzędne punktów 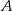 i
i 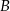 .
.
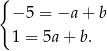
Odejmujemy od drugiego równania pierwsze i mamy 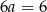 , czyli
, czyli 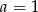 . Stąd
. Stąd 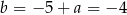 i prosta
i prosta 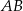 ma równanie:
ma równanie: 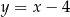 .
.
Dalszą część rozwiązania poprowadzimy na dwa sposoby.
Sposób I
Wysokość trapezu możemy łatwo obliczyć ze wzoru na odległość punktu 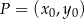 od prostej
od prostej 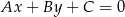 :
:
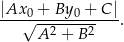
W naszej sytuacji mamy 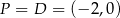 , a prosta to:
, a prosta to: 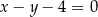 . Mamy zatem
. Mamy zatem
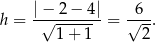
Pole trapezu jest więc równe
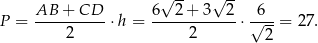
Sposób II
Jeżeli ktoś nie chce korzystać ze wzoru na odległość punktu od prostej, to wysokość trapezu możemy wyznaczyć bardziej wprost, wyznaczając równanie wysokości 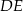 opuszczonej z wierzchołka
opuszczonej z wierzchołka 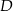 na bok
na bok 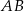 .
.
Prosta 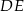 jest prostopadła do prostej
jest prostopadła do prostej 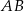 , więc ma równanie postaci
, więc ma równanie postaci 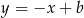 . Współczynnik
. Współczynnik 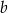 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 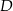 .
.
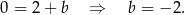
Szukamy teraz punku wspólnego prostych 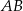 i
i 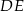 .
.
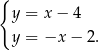
Odejmując od pierwszego równania drugie (żeby skrócić 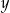 ), mamy
), mamy 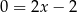 , czyli
, czyli 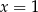 i
i 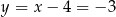 . Zatem
. Zatem 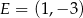 i
i
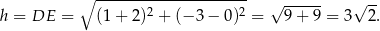
Pole trapezu jest równe
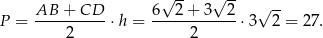
Odpowiedź: 27

