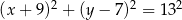Zadanie nr 8907987
Napisz równanie okręgu opisanego na trapezie równoramiennym  , jeżeli
, jeżeli 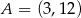 ,
, 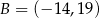 ,
, 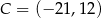 i
i 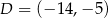 .
.
Rozwiązanie
Szkicujemy trapez.
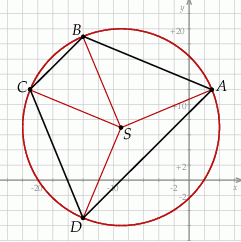
Sposób I
Nie przejmujemy się specjalnie tym, że dany czworokąt jest trapezem równoramiennym i szukamy środka 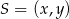 okręgu opisanego tak, aby były spełnione warunki
okręgu opisanego tak, aby były spełnione warunki
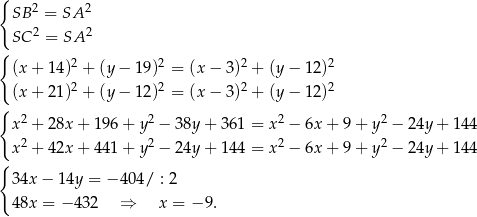
Z pierwszego równania mamy
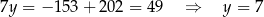
i 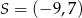 . Obliczamy jeszcze promień
. Obliczamy jeszcze promień 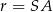 okręgu opisanego
okręgu opisanego
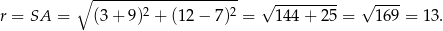
Okrąg opisany na trapezie  ma więc równanie
ma więc równanie
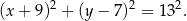
Sposób II
Zauważmy, że punkty  i
i 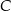 leżą na poziomej prostej
leżą na poziomej prostej 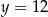 , więc symetralna odcinka
, więc symetralna odcinka 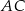 jest pionową prostą o równaniu
jest pionową prostą o równaniu
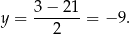
Środek 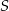 szukanego okręgu oczywiście leży na tej symetralnej, więc jego druga współrzędne jest równa
szukanego okręgu oczywiście leży na tej symetralnej, więc jego druga współrzędne jest równa 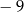 . Podobnie, punkty
. Podobnie, punkty 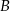 i
i 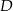 leżą na pionowej prostej
leżą na pionowej prostej 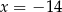 , więc symetralna odcinka
, więc symetralna odcinka 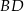 jest poziomą prostą
jest poziomą prostą
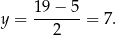
To oznacza, że 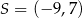 . Promień okręgu opisanego obliczamy tak samo jak w poprzednim sposobie.
. Promień okręgu opisanego obliczamy tak samo jak w poprzednim sposobie.
Odpowiedź: