Zadanie nr 9725386

W trapezie 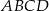ABCD , w którym 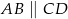AB ∥ CD , dane są wierzchołki 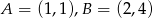A = (1,1),B = (2,4) oraz punkt przecięcia przekątnych 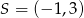S = (− 1,3) . Pole trapezu jest równe 36.

Oblicz długość podstawy .
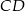Wyznacz współrzędne wierzchołków 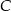i .

Wersja PDF

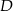Rozwiązanie

Szkicujemy trapez – rysunek może być bardzo schematyczny, tak naprawdę nawet nie trzeba rysować układu współrzędnych.

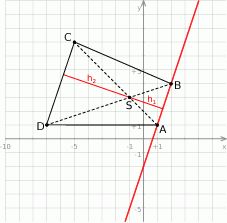
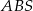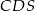Kluczowe w tym zadaniu jest podobieństwo trójkątów ABS i CDS (trójkąty te mają równe kąty).

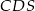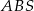Oznaczmy skalę podobieństwa trójkątów i przez 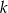. W szczególności 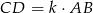oraz 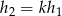, gdzie 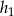i 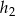są wysokościami tych trójkątów opuszczonymi z wierzchołka 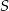. Zauważmy, że 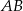i 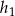możemy dość łatwo obliczyć.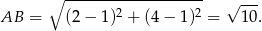
$∘ ------------------- --- AB = (2− 1 )2 + (4 − 1)2 = √ 10.$

Aby obliczyć odległość punktu 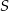od prostej 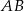najpierw napiszmy równanie prostej 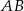. Szukamy prostej w postaci 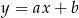. Podstawiamy współrzędne punktów 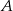i .

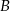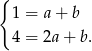
${ 1 = a + b 4 = 2a + b.$

Odejmujemy od drugiego równania pierwsze i mamy 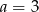. Stad 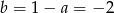. Zatem prosta 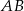ma równanie 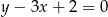. Korzystamy ze wzoru na odległość punktu 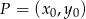od prostej :

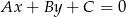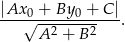
$|Ax-0 +-By0-+-C-| √A--2-+-B2- .$

W naszej sytuacji mamy

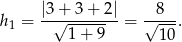
$h1 = |3√+-3-+-2|-= √8--. 1 + 9 10$

Teraz łatwo już wykorzystać informację o polu trapezu – otrzymujemy równanie z niewiadomą .

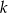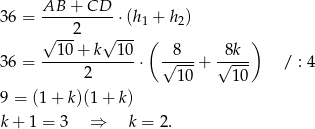
$36 = AB-+--CD--⋅(h + h ) 2 1 2 √ 10+ k√ 10- ( 8 8k ) 36 = -------------⋅ √----+ √---- / : 4 2 10 10 9 = (1 + k)(1 + k) k + 1 = 3 ⇒ k = 2.$

W takim razie .
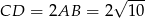Odpowiedź: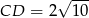
Wiemy już, że skala podobieństwa trójkątów 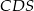i 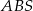jest równa 2. Oznacza to, że 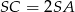i 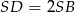. To pozwala łatwo wyznaczyć współrzędne punktów 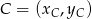i .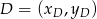
$− → −→ −→ −→ SC = 2AS SD = 2 BS [xC + 1 ,yC − 3] = 2[− 1− 1,3− 1] [xD + 1,yD − 3] = 2[− 1− 2,3− 4] [xC + 1 ,yC − 3] = [− 4,4] [xD + 1,yD − 3] = [− 6,− 2] C = (− 5,7) D = (− 7,1).$

Odpowiedź: