/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Trapez

Zadanie nr 9922027

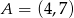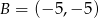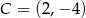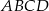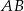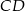Punkty A = (4,7) , B = (− 5,− 5) i C = (2,− 4) są wierzchołkami trapezu prostokątnego ABCD o podstawach AB i CD . Wyznacz współrzędne wierzchołka D .

Wersja PDF

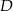Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

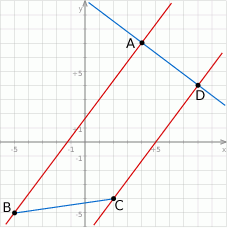
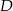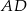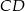Punkt D jest punktem wspólnym prostych AD i CD – spróbujemy wyznaczyć równania tych prostych. Najpierw piszemy równanie prostej 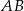AB . Szukamy prostej w postaci 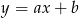y = ax + b i podstawiamy współrzędne punktów 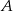A i B .

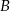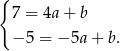
{ 7 = 4a+ b − 5 = − 5a+ b.

Odejmujemy od pierwszego równania drugie (żeby skrócić 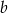b ) i mamy

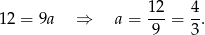
12- 4- 12 = 9a ⇒ a = 9 = 3 .

Współczynnika 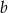b nie musimy obliczać, bo nie jest nam potrzebny. Prosta 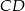CD jest równoległa do 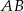AB i przechodzi przez 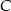C . Szukamy więc prostej w postaci 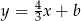4 y = 3x + b i podstawiamy współrzędne punktu C .

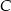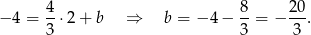
4 8 20 −4 = --⋅2 + b ⇒ b = −4 − --= − ---. 3 3 3

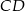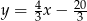Prosta CD ma więc równanie 4 20 y = 3x− 3 .

Prosta 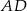AD jest prostopadła do 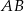AB , więc ma równanie postaci 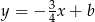y = − 34x + b . Współczynnik 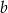b wyznaczamy podstawiając współrzędne punktu A .

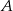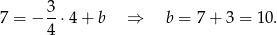
3 7 = − --⋅4 + b ⇒ b = 7+ 3 = 10. 4

Prosta 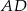AD ma więc równanie 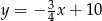y = − 3x + 10 4 i współrzędne punktu 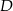D spełniają układ równań

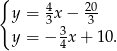
{ 4 20- y = 3x − 3 y = − 34x + 10 .

Odejmujemy od pierwszego równania drugie (żeby skrócić 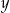y ) i mamy

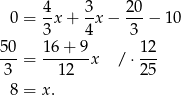
4- 3- 20- 0 = 3x + 4 x− 3 − 10 50 16+ 9 12 ---= ------x /⋅ --- 3 12 25 8 = x .

Stąd 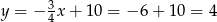y = − 3x + 10 = − 6+ 10 = 4 4 i D = (8 ,4) .  
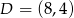Odpowiedź: D = (8,4)

Wersja PDF