Zadanie nr 1067787
Funkcja 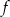 jest określona wzorem
jest określona wzorem 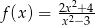 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 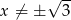 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 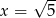 jest równa
jest równa
A) 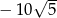 B)
B) 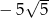 C)
C) 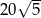 D)
D) 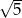
Rozwiązanie
Korzystamy ze wzoru na pochodną ilorazu.
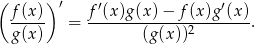
Sposób I
Zauważmy, że
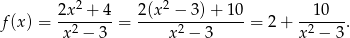
Pochodna tej funkcji jest więc równa
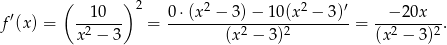
Podstawiamy teraz w tym wzorze 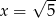 .
.
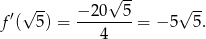
Sposób II
Liczymy pochodną
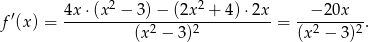
Pochodną w punkcie liczymy tak samo jak w poprzednim sposobie.
Odpowiedź: B

