Zadanie nr 1083631
Granica 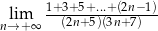 jest równa
jest równa
A) 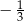 B)
B) 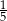 C)
C) 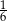 D) 0
D) 0
Rozwiązanie
Zauważmy najpierw, że wyrażenie w liczniku to suma  początkowych wyrazów ciągu arytmetycznego o wyrazie ogólnym
początkowych wyrazów ciągu arytmetycznego o wyrazie ogólnym 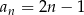 ,
, 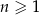 . Zatem
. Zatem
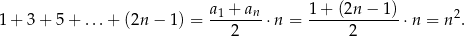
Liczymy teraz granicę – dzielimy licznik i mianownik przez 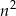 .
.
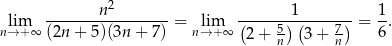
Odpowiedź: C

