Zadanie nr 1129300
Punkt 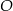 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 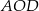 ma miarę
ma miarę
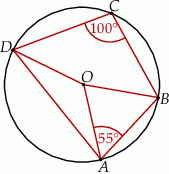
A) 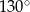 B)
B) 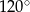 C)
C) 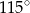 D)
D) 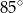
Rozwiązanie
Sposób I
Zauważmy, że trójkąt 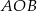 jest równoramienny, więc
jest równoramienny, więc
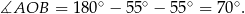
Na mocy twierdzenia o kątach wpisanym i środkowym mamy
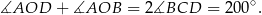
Stąd
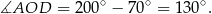
Sposób II
Korzystając z twierdzenia o czworokącie wpisanym w okrąg mamy
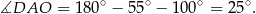
Trójkąt 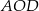 jest równoramienny, więc
jest równoramienny, więc
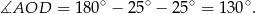
Odpowiedź: A

