Zadanie nr 1170150
Dany jest okrąg o środku 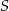 . Punkty
. Punkty 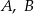 i
i 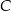 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 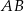 tego okręgu są oparte kąty
tego okręgu są oparte kąty 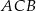 i
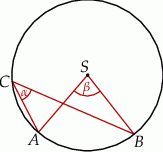
i 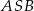 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 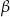 spełniają warunek
spełniają warunek 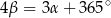 . Wynika stąd, że
. Wynika stąd, że
A) 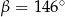 B)
B) 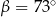 C)
C) 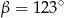 D)
D) 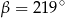
Rozwiązanie
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, mamy
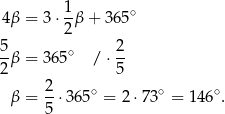
Odpowiedź: A

