Zadanie nr 1199976
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 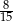 , a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe 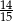 . Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
A) 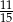 B)
B) 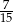 C)
C) 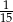 D)
D) 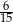
Rozwiązanie
Jeżeli oznaczymy przez 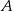 prawdopodobieństwo wylosowania co najmniej jednej kuli białej, a prawdopodobieństwo wylosowania co najwyżej jednej kuli białej przez
prawdopodobieństwo wylosowania co najmniej jednej kuli białej, a prawdopodobieństwo wylosowania co najwyżej jednej kuli białej przez 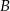 , to suma tych zdarzeń zawiera wszystkie możliwe wyniki (bo zawsze jest albo co najmniej jedna kula biała, albo co najwyżej jedna kula biała). W takim razie
, to suma tych zdarzeń zawiera wszystkie możliwe wyniki (bo zawsze jest albo co najmniej jedna kula biała, albo co najwyżej jedna kula biała). W takim razie
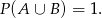
Wiemy ponadto, że 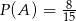 i
i 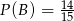 . To co mamy obliczyć to
. To co mamy obliczyć to 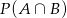 (bo jak jest jednocześnie co najmniej i co najwyżej jedna kula biała to znaczy, że jest dokładnie jedna kula biała). Korzystając ze wzoru
(bo jak jest jednocześnie co najmniej i co najwyżej jedna kula biała to znaczy, że jest dokładnie jedna kula biała). Korzystając ze wzoru
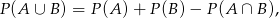
mamy
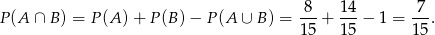
Odpowiedź: B

