Zadanie nr 1313306
Mamy dwie urny. W pierwszej jest 5 kul białych i 5 kul czarnych, w drugiej są 3 kule białe i 7 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z liczbą oczek podzielną przez 3, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest równe
A) 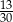 B)
B) 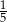 C)
C) 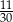 D)
D) 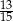
Rozwiązanie
Jeżeli oznaczymy przez 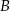 prawdopodobieństwo wylosowania kuli białej w opisanym doświadczeniu losowym, a przez
prawdopodobieństwo wylosowania kuli białej w opisanym doświadczeniu losowym, a przez 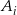 zdarzenie polegające na wyborze urny o numerze
zdarzenie polegające na wyborze urny o numerze 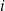 (
(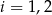 ), to mamy obliczyć prawdopodobieństwo całkowite
), to mamy obliczyć prawdopodobieństwo całkowite
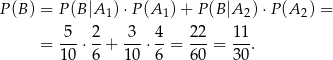
Powyższy rachunek można ładnie zilustrować drzewkiem.
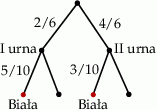
Odpowiedź: C

