Zadanie nr 1354281
Funkcja 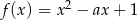 przyjmuje wartości mniejsze niż
przyjmuje wartości mniejsze niż 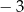 dla
dla
A) 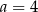 B)
B) 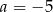 C)
C) 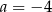 D)
D) 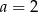
Rozwiązanie
Sposób I
Zapiszmy wzór funkcji 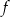 w postaci kanonicznej
w postaci kanonicznej
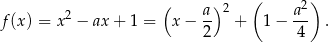
Wykresem tej funkcji jest więc parabola o ramionach skierowanych w górę i wierzchołku w punkcie 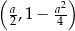 . Jeżeli funkcja ta ma przyjmować wartości mniejsze
. Jeżeli funkcja ta ma przyjmować wartości mniejsze 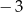 , to musi być spełniony warunek
, to musi być spełniony warunek
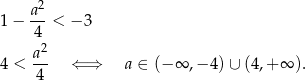
Wśród podanych odpowiedzi tylko 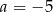 spełnia ten warunek.
spełnia ten warunek.
Sposób II
Wiemy, że nierówność
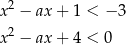
ma rozwiązania, więc musi być
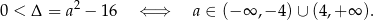
Wśród podanych odpowiedzi tylko 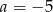 spełnia ten warunek.
spełnia ten warunek.
Sposób III
Wykresem funkcji 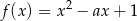 jest parabola o ramionach skierowanych w górę i pierwszej współrzędnej wierzchołka równej
jest parabola o ramionach skierowanych w górę i pierwszej współrzędnej wierzchołka równej
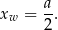
Jeżeli funkcja ma przyjmować wartości mniejsze od 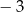 , to wartość w wierzchołku musi być mniejsza od tej liczby
, to wartość w wierzchołku musi być mniejsza od tej liczby
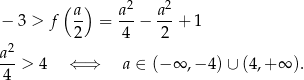
Wśród podanych odpowiedzi tylko 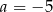 spełnia ten warunek.
spełnia ten warunek.
Odpowiedź: B

