Zadanie nr 1952768
Wykres funkcji kwadratowej 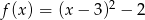 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 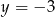 B)
B) 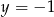 C)
C) 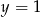 D)
D) 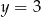
Rozwiązanie
Sposób I
Naszkicujmy parabolę będącą wykresem podanej funkcji: jest to parabola o ramionach skierowanych w górę i wierzchołku w punkcie 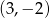 (współrzędne wierzchołka odczytujemy z postaci kanonicznej
(współrzędne wierzchołka odczytujemy z postaci kanonicznej 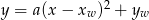 ). Inny sposób, to skorzystanie ze wzoru na przesunięcie wykresu funkcji o wektor: funkcja
). Inny sposób, to skorzystanie ze wzoru na przesunięcie wykresu funkcji o wektor: funkcja 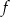 powstaje z wykresu
powstaje z wykresu 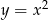 przez przesunięcie o 3 jednostki w prawo i o dwie w dół.
przez przesunięcie o 3 jednostki w prawo i o dwie w dół.
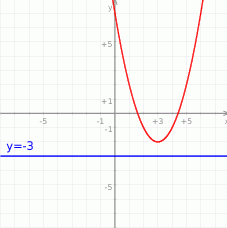
Z obrazka widać, że parabola przecina każdą z podanych prostych z wyjątkiem 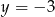 .
.
Sposób II
Ponieważ wykresem podanej funkcji jest parabola o ramionach skierowanych w górę, to jeżeli przecina ona jakąś prostą 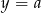 , to przecina też każdą prostą tej postaci z większym
, to przecina też każdą prostą tej postaci z większym  . Z tego powodu jedyną poprawną odpowiedzią może być A (bo wiemy, że tylko jedna odpowiedź jest poprawna).
. Z tego powodu jedyną poprawną odpowiedzią może być A (bo wiemy, że tylko jedna odpowiedź jest poprawna).
Odpowiedź: A

