Zadanie nr 2066965
Punkt 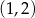 jest wierzchołkiem paraboli o równaniu
jest wierzchołkiem paraboli o równaniu
A) 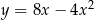 B)
B) 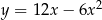 C)
C) 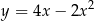 D)
D) 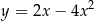
Rozwiązanie
Zauważmy, że
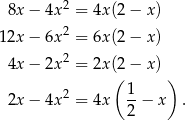
Ponieważ wierzchołek paraboli znajduje się dokładnie w środku między pierwiastkami, to eliminuje to odpowiedź 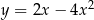 . Pierwsza współrzędna wierzchołka dla pozostałych parabol jest równa
. Pierwsza współrzędna wierzchołka dla pozostałych parabol jest równa 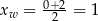 . Teraz wystarczy sprawdzić, dla którego ze wzorów spełniony jest warunek
. Teraz wystarczy sprawdzić, dla którego ze wzorów spełniony jest warunek
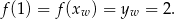
Gdy to zrobimy, okaże się, że warunek ten spełnia wzór 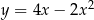 .
.
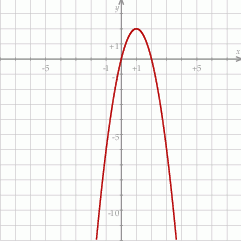
Odpowiedź: C

