Zadanie nr 2069565
Dany jest okrąg o środku w punkcie 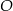 . Prosta
. Prosta 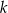 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 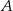 .
.
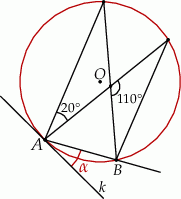
Miara kąta  jest równa
jest równa
A) 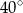 B)
B) 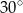 C)
C) 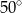 D)
D) 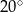
Rozwiązanie
Opiszmy trochę dany rysunek.
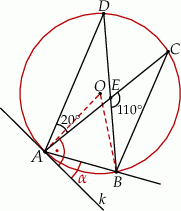
Zauważmy, że łatwo możemy obliczyć miarę kąta wpisanego 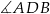 . Patrzymy na trójkąt
. Patrzymy na trójkąt 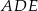 .
.
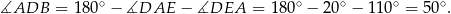
Sposób I
Kąt środkowy 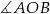 jest oparty na tym samym łuku, co kąt wpisany
jest oparty na tym samym łuku, co kąt wpisany 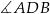 , więc
, więc
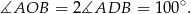
Odcinki 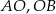 są promieniami okręgu, więc trójkąt
są promieniami okręgu, więc trójkąt 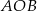 jest równoramienny. Zatem
jest równoramienny. Zatem
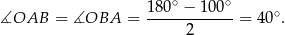
Teraz wystarczy zauważyć, że styczna 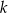 jest prostopadła do promienia
jest prostopadła do promienia 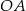 , więc
, więc
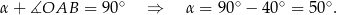
Sposób II
Korzystamy z twierdzenia o stycznej:
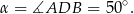
Odpowiedź: C

