Zadanie nr 2110773
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 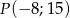 .
.
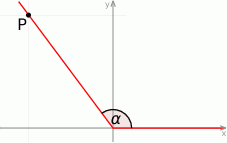
Zatem 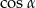 jest równy
jest równy
A) 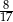 B)
B) 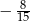 C)
C) 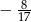 D)
D) 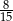
Rozwiązanie
Niech 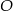 będzie początkiem układu współrzędnych, a
będzie początkiem układu współrzędnych, a 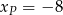 pierwszą współrzędną punktu
pierwszą współrzędną punktu 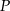 .
.
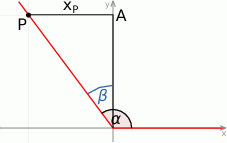
Sposób I
Korzystamy z definicji cosinusa.
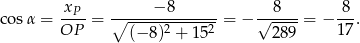
Sposób II
Jeżeli 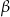 jest kątem jaki promień
jest kątem jaki promień 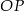 tworzy z osią
tworzy z osią 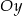 to mamy
to mamy
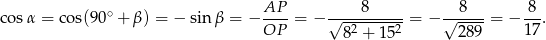
Odpowiedź: C

