Zadanie nr 2284272
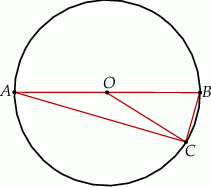
Odcinek 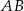 jest średnicą okręgu o środku
jest średnicą okręgu o środku 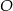 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 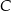 , taki, że
, taki, że 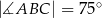 (zobacz rysunek).
(zobacz rysunek).
Pole trójkąta 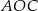 jest równe
jest równe
A) 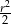 B)
B) 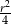 C)
C) 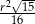 D)
D) 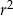
Rozwiązanie
Sposób I
Trójkąt 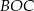 jest równoramienny więc
jest równoramienny więc
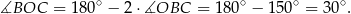
Stąd
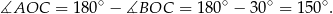
Korzystamy teraz ze wzoru z sinusem na pole trójkąta
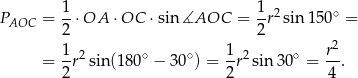
Sposób II
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, mamy
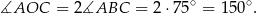
Pole trójkąta  obliczamy tak samo jak w pierwszym sposobie.
obliczamy tak samo jak w pierwszym sposobie.
Odpowiedź: B

