/Szkoła średnia/Zadania testowe

Zadanie nr 2285634

Dodaj do ulubionych
Dodaj do rozwiązanych

Każdą krawędź czworościanu foremnego skracamy trzykrotnie. Pole powierzchni czworościanu zmniejszy się
A) trzykrotnie B) sześciokrotnie C) dwudziestosiedmiokrotnie D) dziewięciokrotnie

Rozwiązanie

Sposób I

Ponieważ pole powierzchni zmienia się jak kwadrat skali podobieństwa pole powierzchni zmniejszy się 9 razy.

Sposób II

Przypomnijmy, że każda ze ścian czworościanu foremnego jest identycznym trójkątem równobocznym. Oznaczmy przez a długość krawędzi trójkąta. Pole trójkąta równobocznego jest dana wzorem

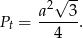
√ -- a2--3- Pt = 4 .

Zatem pole całkowite czworościanu jest równe

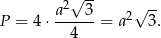
√ -- a2 3 2√ -- P = 4⋅ ------= a 3. 4

Obliczamy pole powierzchni powiększonego czworościanu

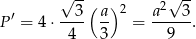
√ -- √ -- ′ 3 (a )2 a2 3 P = 4⋅ ---- -- = ------. 4 3 9

Stąd

′ P P = 9.

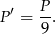
Zatem pole powierzchni zmniejszyło się dziewięciokrotnie.  
Odpowiedź: D

Wersja PDF