Zadanie nr 2353283
Prosta o równaniu 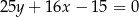 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji 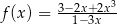 w punkcie
w punkcie
A) 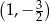 B)
B) 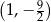 C)
C) 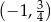 D)
D) 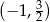
Rozwiązanie
Dana prosta ma współczynnik kierunkowy równy 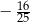 , więc musimy sprawdzić, w którym z podanych punktów pochodna danej funkcji jest równa
, więc musimy sprawdzić, w którym z podanych punktów pochodna danej funkcji jest równa 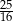 . Liczymy tą pochodną
. Liczymy tą pochodną
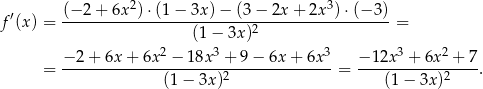
Sprawdzamy teraz, że
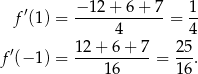
W takim razie interesuje nas punkt z pierwszą współrzędną równą 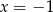 . Sprawdzamy jeszcze, że
. Sprawdzamy jeszcze, że
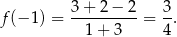
Interesująca nas styczna jest więc styczna do wykresu funkcji w punkcie 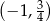 .
.
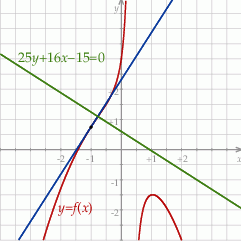
Odpowiedź: C

