/Szkoła średnia/Zadania testowe

Zadanie nr 2609324

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile wyrazów ma ciąg geometryczny 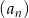(an) , w którym 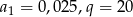a1 = 0,025,q = 20 , natomiast ostatni wyraz jest równy 4000?
A) 3 B) 4 C) 5 D) 6

Rozwiązanie

Zauważmy, że

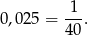
1 0,025 = --. 40

Sposób I

Liczymy kolejne wyrazy ciągu

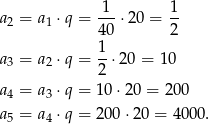
-1- 1- a2 = a1 ⋅q = 40 ⋅20 = 2 1 a3 = a2 ⋅q = --⋅20 = 1 0 2 a4 = a3 ⋅q = 10⋅ 20 = 200 a5 = a4 ⋅q = 200 ⋅20 = 40 00.

Sposób II

Szukamy takiego n , że

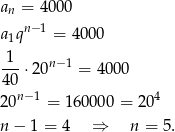
a = 4 000 n a1qn− 1 = 4000 1 ---⋅20n −1 = 400 0 40 20n− 1 = 16000 0 = 204 n − 1 = 4 ⇒ n = 5.

Sposób III

Rozpisujemy liczbę 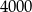400 0

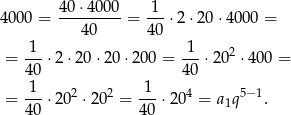
40-⋅4000- -1- 4000 = 40 = 40 ⋅2 ⋅20 ⋅4000 = 1 1 = ---⋅ 2⋅20 ⋅20 ⋅200 = ---⋅202 ⋅400 = 4 0 40 -1- 2 2 -1- 4 5−1 = 4 0 ⋅ 20 ⋅2 0 = 40 ⋅20 = a1q .

 
Odpowiedź: C

Wersja PDF