Zadanie nr 2658278
Równanie 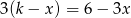 z niewiadomą
z niewiadomą  ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 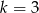 B)
B) 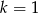 C)
C) 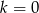 D)
D) 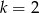
Rozwiązanie
Sposób I
Dane równanie możemy zapisać w postaci
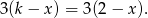
Widać teraz, że jeżeli tylko 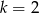 to równanie jest spełnione przez dowolną liczbę rzeczywistą.
to równanie jest spełnione przez dowolną liczbę rzeczywistą.
Sposób II
Próbujemy rozwiązać dane równanie.
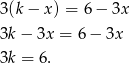
Widać teraz, że jeżeli 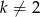 to równanie jest sprzeczne, a jeżeli
to równanie jest sprzeczne, a jeżeli 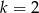 to równanie spełnia każda liczba rzeczywista.
to równanie spełnia każda liczba rzeczywista.
Odpowiedź: D

