Zadanie nr 2661146
Punkt 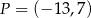 przekształcono w symetrii względem symetralnej odcinka o końcach
przekształcono w symetrii względem symetralnej odcinka o końcach 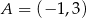 i
i 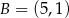 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 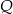 . Zatem długość odcinka
. Zatem długość odcinka 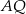 jest równa
jest równa
A) 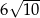 B)
B) 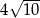 C)
C) 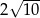 D)
D) 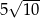
Rozwiązanie
Robimy szkicowy rysunek.
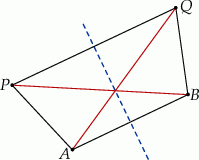
Zauważmy, że symetralna odcinka 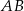 jest osią symetrii czworokąta o wierzchołkach
jest osią symetrii czworokąta o wierzchołkach 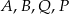 , czyli jest to trapez równoramienny i
, czyli jest to trapez równoramienny i
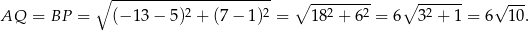
Odpowiedź: A

