Zadanie nr 2773382
Wielomiany 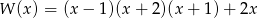 i
i 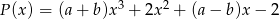 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 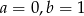 B)
B) 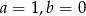 C)
C) 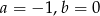 D)
D) 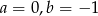
Rozwiązanie
Przekształcamy wielomian 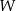
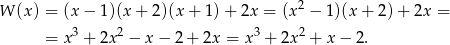
Wielomiany są równe jeżeli współczynniki przy odpowiadających sobie potęgach zmiennej  są równe. Rozwiązujemy układ równań
są równe. Rozwiązujemy układ równań
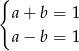
Dodając równania stronami mamy 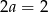 , czyli
, czyli 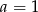 . Stąd
. Stąd 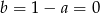 .
.
Odpowiedź: B

