Zadanie nr 2776174
Objętość ostrosłupa prawidłowego czworokątnego jest równa 270, a pole jego podstawy jest równe 81. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 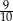 B)
B) 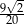 C)
C) 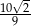 D)
D) 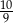
Rozwiązanie
Zaczynamy od rysunku
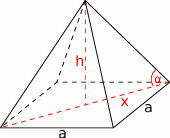
Ze wzoru na objętość wyznaczamy długość wysokości
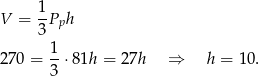
Ze wzoru na pole podstawy wyznaczamy długość krawędzi 
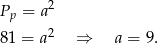
Szukany tangens to stosunek długości wysokości do połowy przekątnej podstawy, czyli
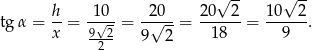
Odpowiedź: C

