/Szkoła średnia/Zadania testowe

Zadanie nr 2851787

Dodaj do ulubionych
Dodaj do rozwiązanych

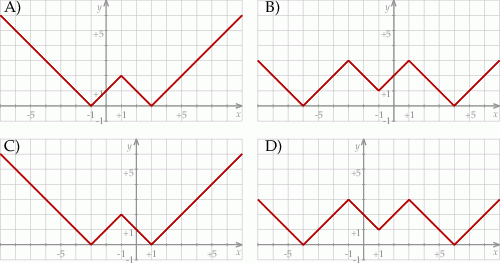
Wskaż rysunek, na którym przedstawiono fragment wykresu funkcji

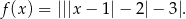
f(x ) = |||x − 1|− 2|− 3 |.

PIC

Rozwiązanie

Sposób I

Zauważmy, że

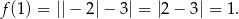
f(1) = ||− 2| − 3| = |2− 3| = 1.

Taka sytuacja ma miejsce tylko na wykresie D.

Sposób II

Sprawdźmy jakie są miejsca zerowe danej funkcji

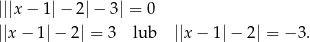
|||x− 1|− 2| − 3| = 0 ||x − 1|− 2| = 3 lub ||x − 1|− 2| = − 3.

Druga możliwość jest sprzeczna, więc

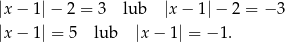
|x − 1|− 2 = 3 lub |x− 1|− 2 = − 3 |x − 1| = 5 lub |x− 1| = − 1.

Ponownie druga możliwość jest sprzeczna, więc mamy

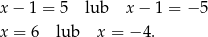
x− 1 = 5 lub x − 1 = − 5 x = 6 lub x = − 4 .

Wykres z takimi miejscami zerowymi to wykres D.

Sposób III

Szkicujemy wykres funkcji 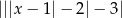|||x − 1|− 2|− 3 | – zaczynamy od prostej 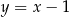y = x − 1 i odbijamy część poniżej osi 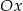Ox do góry.

PIC

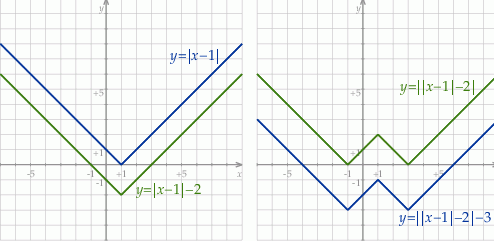
Potem otrzymany wykres przesuwamy o 2 jednostki w dół i znowu odbijamy część poniżej osi 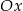Ox do góry. Na koniec przesuwamy wykres o 3 jednostki w dół i ponownie odbijamy część poniżej osi 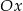Ox do góry. Otrzymamy w ten sposób wykres z rysunku D.  
Odpowiedź: D

Wersja PDF