/Szkoła średnia/Zadania testowe

Zadanie nr 2865126

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód trójkąta prostokątnego równoramiennego wynosi 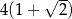√ -- 4(1 + 2) . Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
A) 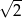√ -- 2 B) 4 C) 2 D)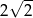 √ -- 2 2

Rozwiązanie

Jeżeli przez a oznaczymy długość przyprostokątnej takiego trójkąta, to jego przeciwprostokątna ma długość √ -- a 2 .

PIC

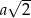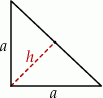
Sposób I

Z podanego obwodu mamy

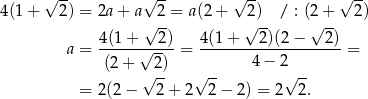
√ -- √ -- √ -- √ -- 4(1+ 2) = 2a + a 2 = a (2+ 2) / : (2 + 2) 4(1 + √ 2) 4(1 + √ 2)(2 − √ 2) a = ------√----= --------------------= (2+ 2) 4 − 2 √ -- √ -- √ -- = 2(2 − 2 + 2 2 − 2) = 2 2.

Porównujemy teraz dwa wzory na pole trójkąta

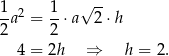
1 1 √ -- --a2 = --⋅a 2 ⋅h 2 2 4 = 2h ⇒ h = 2.

Sposób II

Dany trójkąt to połówka kwadratu, więc jego przeciwprostokątna ma długość 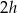2h oraz

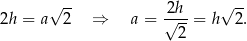
√ -- √ -- 2h = a 2 ⇒ a = √2h-= h 2. 2

Z podanego obwodu mamy

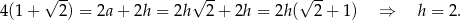
√ -- √ -- √ -- 4(1 + 2) = 2a+ 2h = 2h 2+ 2h = 2h( 2 + 1 ) ⇒ h = 2.

 
Odpowiedź: C

Wersja PDF