Zadanie nr 2882780
Liczba 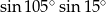 jest równa
jest równa
A) 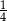 B)
B) 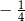 C)
C) 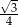 D)
D) 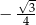
Rozwiązanie
Sposób I
Korzystamy ze wzorów
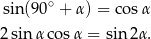
Liczymy
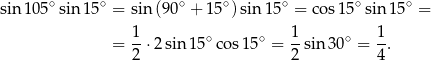
Sposób II
Korzystamy ze wzoru
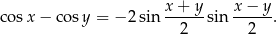
Mamy zatem
![∘ ∘ 1 ∘ ∘ ∘ ∘ sin 105 sin1 5 = − 2-⋅[− 2sin(6 0 + 45 )sin (60 − 45 )] = ( ∘ ∘ ∘ ∘) = − 1-⋅ − 2sin 120--+-90--sin 1-20-−-90- = 2 2 2 1 1 ( 1 ) 1 = − --⋅(cos 120∘ − cos9 0∘) = − -- − --− 0 = --. 2 2 2 4](https://img.zadania.info/zad/2882780/HzadR3x.gif)
Odpowiedź: A
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Liczba 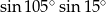 jest równa
jest równa
A) 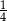 B)
B) 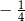 C)
C) 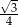 D)
D) 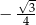
Sposób I
Korzystamy ze wzorów
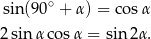
Liczymy
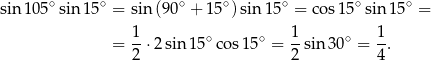
Sposób II
Korzystamy ze wzoru
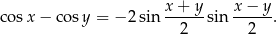
Mamy zatem
![∘ ∘ 1 ∘ ∘ ∘ ∘ sin 105 sin1 5 = − 2-⋅[− 2sin(6 0 + 45 )sin (60 − 45 )] = ( ∘ ∘ ∘ ∘) = − 1-⋅ − 2sin 120--+-90--sin 1-20-−-90- = 2 2 2 1 1 ( 1 ) 1 = − --⋅(cos 120∘ − cos9 0∘) = − -- − --− 0 = --. 2 2 2 4](https://img.zadania.info/zad/2882780/HzadR3x.gif)
Odpowiedź: A
