Zadanie nr 2936124
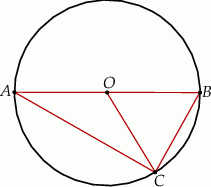
Odcinek 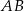 jest średnicą okręgu o środku
jest średnicą okręgu o środku 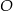 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 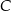 , taki, że
, taki, że 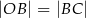 (zobacz rysunek).
(zobacz rysunek).
Pole trójkąta 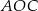 jest równe
jest równe
A) 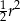 B)
B) 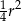 C)
C) 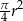 D)
D) 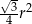
Rozwiązanie
Zauważmy, że w trójkącie 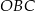 mamy
mamy
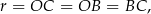
więc jest to trójkąt równoboczny. W takim razie 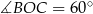 .
.
Sposób I
Trójkąty 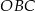 i
i 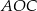 mają podstawy
mają podstawy 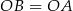 równej długości oraz wspólną wysokość opuszczoną na te podstawy. Mają więc równe pola
równej długości oraz wspólną wysokość opuszczoną na te podstawy. Mają więc równe pola
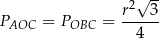
(korzystamy ze wzoru na pole trójkąta równobocznego.)
Sposób II
Korzystamy ze wzoru z sinusem na pole trójkąta
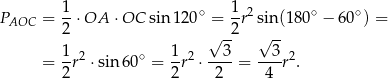
Odpowiedź: D

