/Szkoła średnia/Zadania testowe

Zadanie nr 2946925

Dodaj do ulubionych
Dodaj do rozwiązanych

Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 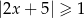|2x + 5| ≥ 1 .

PIC

Rozwiązanie

Sposób I

Liczba 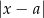|x− a| jest równa odległości liczb x i a na osi liczbowej. Przekształćmy daną nierówność tak, aby miała taką postać.

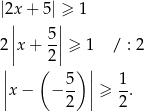
|2x| + 5| ≥| 1 | 5| 2 ||x + -|| ≥ 1 / : 2 | ( 2 )| || 5- || 1- |x − − 2 | ≥ 2 .

Zatem dana nierówność jest spełniona przez liczby x , których odległość od -2,5 jest nie mniejsza niż 0,5. Jest to więc zbiór

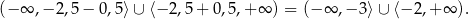
(− ∞ ,−2 ,5− 0 ,5⟩∪ ⟨− 2,5 + 0,5,+ ∞ ) = (− ∞ ,− 3⟩ ∪ ⟨− 2,+ ∞ ).

Sposób II

Rozwiązujemy nierówność

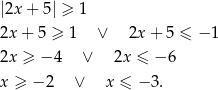
|2x+ 5| ≥ 1 2x + 5 ≥ 1 ∨ 2x+ 5 ≤ − 1 2x ≥ − 4 ∨ 2x ≤ − 6 x ≥ − 2 ∨ x ≤ − 3.

 
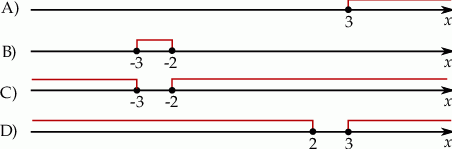
Odpowiedź: C

Wersja PDF