Zadanie nr 3037932
Granica 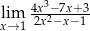 jest równa
jest równa
A) 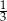 B)
B)  C)
C) 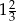 D)
D) 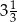
Rozwiązanie
Wstawiając 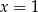 do licznika i mianownika łatwo się przekonać, że mamy do czynienia z wyrażeniem postaci
do licznika i mianownika łatwo się przekonać, że mamy do czynienia z wyrażeniem postaci  . Skoro obydwa wielomiany zerują się w
. Skoro obydwa wielomiany zerują się w 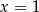 , to muszą się dzielić przez
, to muszą się dzielić przez 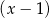 . Wykonajmy to dzielenie (my zrobimy to grupując wyrazy).
. Wykonajmy to dzielenie (my zrobimy to grupując wyrazy).
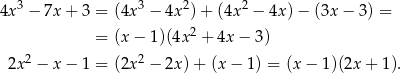
Zatem
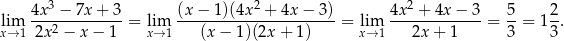
Odpowiedź: C

