Zadanie nr 3062273
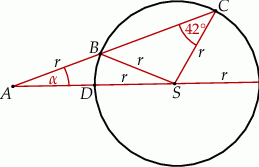
Punkty 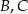 i
i 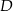 leżą na okręgu o środku
leżą na okręgu o środku 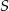 i promieniu
i promieniu  . Punkt
. Punkt 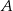 jest punktem wspólnym prostych
jest punktem wspólnym prostych 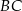 i
i 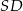 , a odcinki
, a odcinki 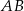 i
i 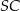 są równej długości. Miara kąta
są równej długości. Miara kąta 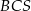 jest równa
jest równa 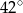 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
A) 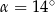 B)
B) 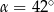 C)
C) 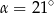 D)
D) 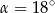
Rozwiązanie
Trójkąty 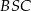 i
i  są równoramienne, więc
są równoramienne, więc
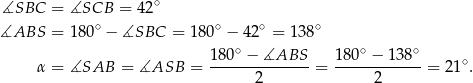
Odpowiedź: C

