Zadanie nr 3185218
Pole trójkąta 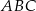 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
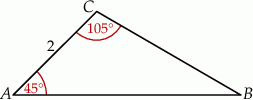
A) 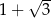 B)
B) 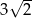 C)
C) 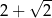 D)
D) 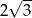
Rozwiązanie
Sposób I
Dorysujmy wysokość 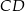 opuszczoną na bok
opuszczoną na bok 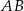 .
.
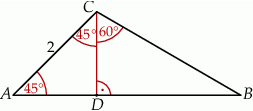
Trójkąt 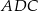 to połówka kwadratu, a trójkąt
to połówka kwadratu, a trójkąt 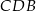 to połówka trójkąta równobocznego o boku
to połówka trójkąta równobocznego o boku 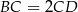 . Mamy zatem
. Mamy zatem
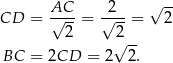
Stąd
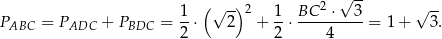
Sposób II
Obliczamy najpierw miarę trzeciego kąta trójkąta.
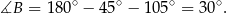
Na mocy twierdzenia sinusów mamy
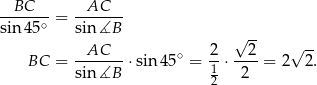
Zauważmy jeszcze, że
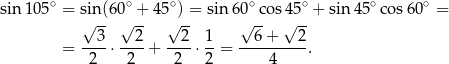
Pole trójkąta jest więc równe
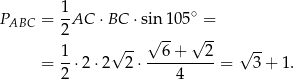
Odpowiedź: A

