/Szkoła średnia/Zadania testowe

Zadanie nr 3209181

Dodaj do ulubionych
Dodaj do rozwiązanych

Szereg geometryczny:

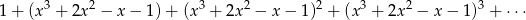
3 2 3 2 2 3 2 3 1+ (x + 2x − x − 1) + (x + 2x − x − 1) + (x + 2x − x − 1) + ⋅⋅⋅

jest zbieżny dla
A) 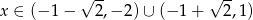√ -- √ -- x ∈ (− 1 − 2,− 2) ∪ (− 1+ 2,1)
B) 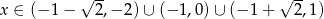√ -- √ -- x ∈ (− 1− 2,− 2)∪ (− 1,0 )∪ (− 1 + 2,1)
C) 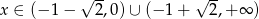√ -- √ -- x ∈ (− 1 − 2,0) ∪ (− 1+ 2,+ ∞ )
D) 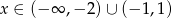x ∈ (− ∞ ,− 2) ∪ (− 1,1)

Rozwiązanie

Sprawdzamy, kiedy iloraz 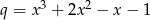3 2 q = x + 2x − x − 1 spełnia nierówność |q| < 1 .

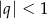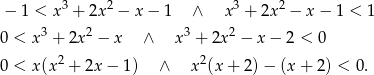
3 2 3 2 − 1 < x + 2x − x− 1 ∧ x + 2x − x − 1 < 1 0 < x3 + 2x2 − x ∧ x3 + 2x 2 − x − 2 < 0 0 < x(x2 + 2x − 1) ∧ x 2(x+ 2)− (x + 2) < 0.

Rozłóżmy trójmian w pierwszym nawiasie

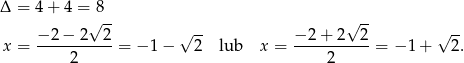
Δ = 4 + 4 = 8 √ -- √ -- √ -- √ -- x = −-2-−-2--2-= − 1− 2 lub x = −-2-+-2--2-= − 1 + 2. 2 2

Rozwiązaniem pierwszej nierówności jest więc zbiór

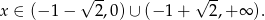
√ -- √ -- x ∈ (− 1 − 2,0) ∪ (− 1+ 2,+ ∞ ).

Rozwiązujemy teraz drugą nierówność

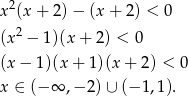
x2(x + 2) − (x + 2) < 0 2 (x − 1)(x + 2) < 0 (x − 1)(x + 1)(x + 2 ) < 0 x ∈ (− ∞ ,− 2) ∪ (− 1,1).

Częścią wspólną obu rozwiązań jest zbiór

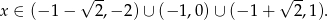
√ -- √ -- x ∈ (− 1− 2,− 2)∪ (− 1,0) ∪ (− 1+ 2,1).

 
Odpowiedź: B

Wersja PDF