/Szkoła średnia/Zadania testowe

Zadanie nr 3439938

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja określona wzorem 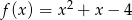2 f (x ) = x + x − 4 nie przyjmuje wartości
A) -5 B) -4 C) 0 D) 2

Rozwiązanie

Sposób I

Sprawdzamy ile pierwiastków ma funkcja

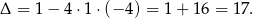
Δ = 1 − 4 ⋅1 ⋅(− 4) = 1 + 16 = 1 7.

Wyznaczamy współrzędne wierzchołka 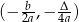b Δ (− 2a,− 4a)

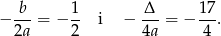
b 1 Δ 17 − ---= − -- i − ---= − ---. 2a 2 4a 4

Teraz łatwo naszkicować parabolę będącą wykresem funkcji f .

PIC

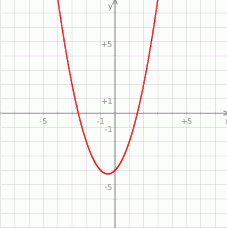
Odpowiedź odczytujemy z wykresu.

Sposób II

Skoro wykresem podanej funkcji jest parabola o ramionach skierowanych w górę, oraz wiemy, że tylko jedna odpowiedź jest poprawna, to musi to być odpowiedź -5 (bo gdyby -5 było wartością, to każda większa liczba też byłaby wartością funkcji).

Sposób III

Sprawdzamy które równanie jest sprzeczne

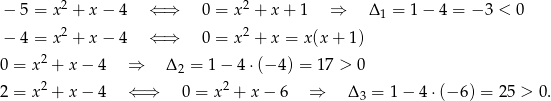
2 2 − 5 = x + x − 4 ⇐ ⇒ 0 = x + x+ 1 ⇒ Δ 1 = 1− 4 = − 3 < 0 − 4 = x2 + x − 4 ⇐ ⇒ 0 = x2 + x = x(x + 1) 2 0 = x + x − 4 ⇒ Δ2 = 1 − 4 ⋅(− 4) = 17 > 0 2 = x2 + x − 4 ⇐ ⇒ 0 = x2 + x − 6 ⇒ Δ = 1 − 4 ⋅(− 6) = 25 > 0 . 3

Z powyższego widzimy, że tylko pierwsze równanie nie ma rozwiązania.  
Odpowiedź: A

Wersja PDF