Zadanie nr 3501243
Niech 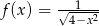 . Dziedziną funkcji
. Dziedziną funkcji 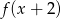 jest zbiór
jest zbiór
A) 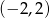 B)
B) 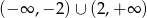 C)
C) 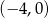 D)
D) 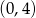
Rozwiązanie
Sposób I
Sprawdźmy jaka jest dziedzina funkcji 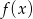 , czyli kiedy wyrażenie pod pierwiastkiem jest dodatnie.
, czyli kiedy wyrażenie pod pierwiastkiem jest dodatnie.
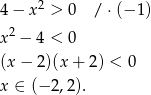
Wykres funkcji 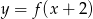 powstaje z wykresu funkcji
powstaje z wykresu funkcji 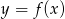 przez przesunięcie o 2 jednostki w lewo, zatem jej dziedziną jest przedział
przez przesunięcie o 2 jednostki w lewo, zatem jej dziedziną jest przedział 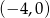 .
.
Sposób II
Funkcja 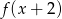 ma wzór
ma wzór
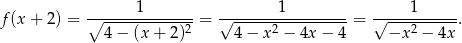
Pozostało sprawdzić, kiedy wyrażenie pod pierwiastkiem jest dodatnie
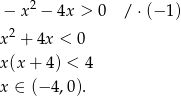
Odpowiedź: C

